开发工具|matlab查询文档

matlab算数运算

快速查询：算术运算 - MATLAB & Simulink - MathWorks 中国

1.基本运算

符号	解释
.*	乘法
*	矩阵乘法
./	数组右除
.\	数组左除
x = B/A	对线性方程组 xA = B 求解 x（矩阵适用）
x=A\B	对线性方程组 Ax = B 求解 x（矩阵适用）
b = mod(`a`,`m`)	返回 `a` 除以 `m` 后的余数，其中 `a` 是被除数，`m` 是除数

2.基本数数学函数

快速查询：Matlab常用数学函数和数学运算符_cc198877的专栏-CSDN博客_matlab数学运算符

matlab数组与矩阵运算

矩阵运算遵循线性代数的法则。与之不同，数组运算则是执行逐元素运算并支持多维数组

快速查询：数组与矩阵运算 - MATLAB & Simulink - MathWorks 中国

1.矩阵加法

由于矩阵运算和数组运算在加法和减法的运算上相同，因此没有必要使用字符组合 .+ 和 .-。

2.矩阵数乘

3.矩阵乘法

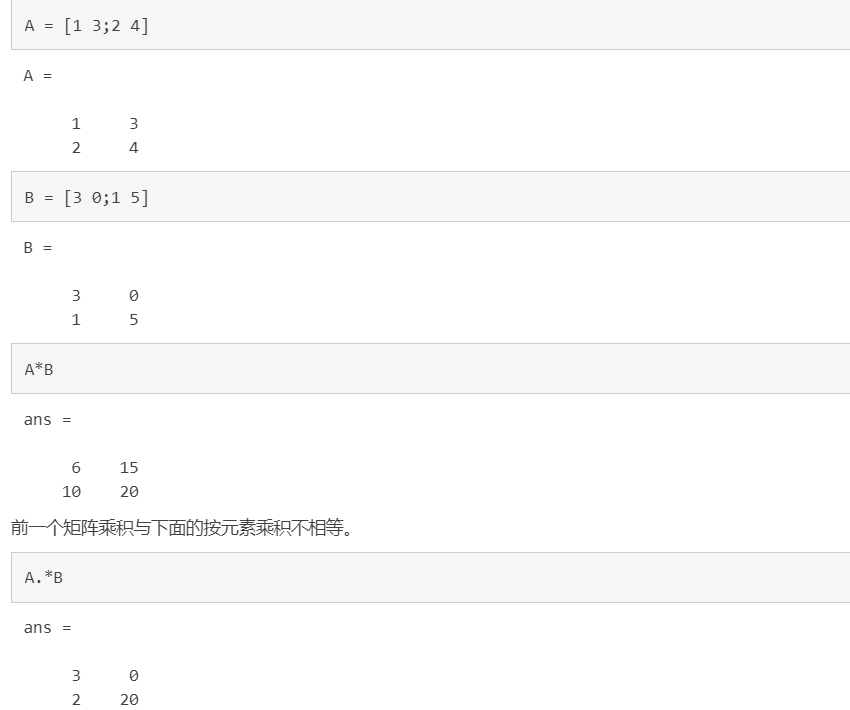
4.数组运算

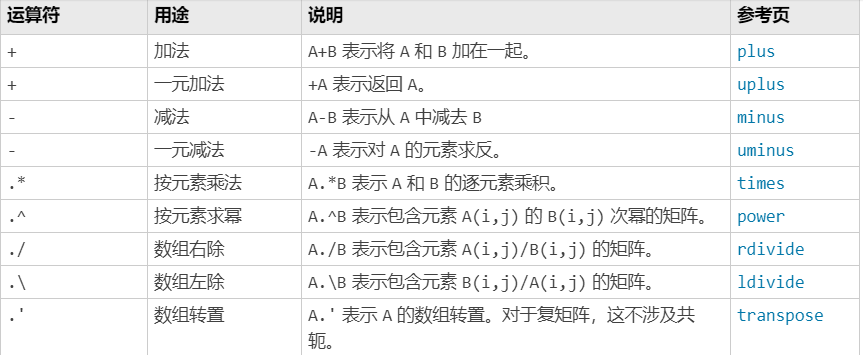
5.矩阵运算

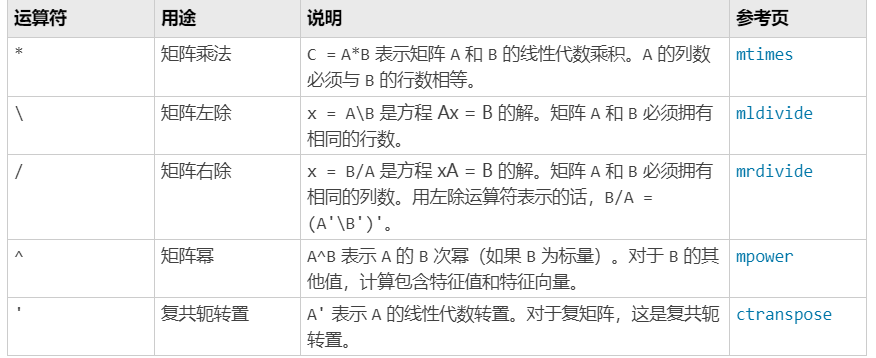
矩阵简单操作

快速查询：矩阵和数组 - MATLAB & Simulink - MathWorks 中国

详细总结：matlab矩阵的表示和简单操作 - Hello_Word - 博客园 (cnblogs.com)

1.矩阵创建

（1）直接输入法

（2）利用MATLAB函数创建矩阵

常用的如下

ones()函数：产生全为1的矩阵，ones(n)：产生nn维的全1矩阵，ones(m,n)：产生mn维的全1矩阵；
zeros()函数：产生全为0的矩阵；
rand()函数：产生在（0，1）区间均匀分布的随机阵；
eye()函数：产生单位阵；
randn()函数：产生均值为0，方差为1的标准正态分布随机矩阵。

（3）利用运算确定范围

如：产生一个均匀分布在（-5，5）之间的随即矩阵（10×2）

function A = my()
    A = -5 + 10 * rand(10,2);
    A = roundn(A,-1);
end

2.矩阵索引

（1）索引矩阵中一个元素

1 2	# 表示索引A矩阵第i行、第j列的元素 A(i,j)

（2）遍历一个矩阵中所有元素

一般用例：

A = randn(3,4)     % 创建3行4列随机矩阵
[r,c] = size(A)    % 读取行r、列c
for i = 1:r        % 建立for循环嵌套
    for k = 1:c
        A(i,k)     % 读取矩阵每个位置数据，先行后列
    end
end

find方法（查找非零元素的索引和值）：

# k = find(X) 返回一个包含数组 X 中每个非零元素的线性索引的向量，用length可以统计个数
X = [18 3 1 11; 8 10 11 3; 9 14 6 1; 4 3 15 21]
# 通过find查找矩阵中的所有符合条件的元素，并把其索引组成数组
[row,col] = find(X>0 & X<10)

实用案例：

# 需要用到两个循环来遍历元素
a = [
0, 1, 5, -2, 8;
3, -4, 9, 3, -8;
0, 3, 6, 2, -1;
0, 0, 55, 1, -2;
];
# 创建一个空矩阵存储符合条件的元素
b  = [];

for i = 1:4
    for j = 1:5
        if a(i,j) > 1
        # 矩阵添加元素（子矩阵）的方法
            b = [b a(i,j)];
        end    
    end    
end 
disp(b);

3.矩阵拆分和组合

（1）组合（串联）

# 将两个行向量串联起来，形成一个更长的行向量
A = ones(1,4);
B = zeros(1,4);
C = [A B]

1 2	# 将 A 和 B 排列为一个矩阵的两行 D = [A;B]

（2）拆分（取出一个子矩阵）

A(:,j) # 表示取A矩阵的第j列全部元素
A(i,:) # 表示A矩阵第i行的全部元素
A(i:i+m,:) # 表示取A矩阵第i~i+m行的全部元素
A(i:i+m,k:k+m) # 表示取A矩阵第i~i+m行内，并在第k~k+m列中的所有元素

4.矩阵的相关计算

v为矩阵的特征值，d为特征向量

a = [1,1,0.5; 1,1,0.25; 0.5,0.25,2;];
[v,d] = eig(a);
disp(v);
disp(d);

MATLAB的图形绘制

快速查询：https://ww2.mathworks.cn/help/matlab/learn_matlab/basic-plotting-functions.html#responsive_offcanvas

一.绘制一般曲线（二维线图）

# x定周期，通过加减表示无意义点
x = [0:0.01:pi/2-0.01, pi/2+0.01:0.01:(3*pi/2)-0.01, (3*pi/2)+0.01:0.01:2*pi];
# 定义y的函数（此处分别为正割和余割）
y1 = sec(x);
y2 = csc(x);

# subplot 命令用于在同一窗口中显示多个绘图，此处表示的意思是将窗口划分为2*1（即上下两幅图），并选择第一处
subplot(2,1,1)
# 绘制图形，r-表示绘制红色点划线
plot(x,y1,'r-.')
# 注意要绘制完图形后，才能加上标注
xlabel('x')
ylabel('y')
title('正割公式')

# 选定第二处绘图
subplot(2,1,2)
plot(x,y2,'b')
xlabel('x')
ylabel('y')
title('余割公式')
# axis设置坐标轴范围，x为0-3，y为0-12
axis([0 3 0 12]);

二.绘制极坐标曲线

快速查询：https://ww2.mathworks.cn/help/matlab/ref/polarplot.html#d122e940353

# theta参数为极坐标曲线的角度值，此处表示从0-2pi
theta = 0:0.01:2*pi;
# input输入数据
a = input('a=');
b = input('b=');
n = input('n=');
# rho参数为半径值，即极坐标曲线的ρ
rho = a*sin(b+n*theta);
# 生成曲线图，r设定曲线为红色
polarplot(theta,rho,'r');

三.绘制曲面图

# meshgrid(x,y)基于向量 x 和 y 中包含的坐标返回二维网格坐标
[x, y] = meshgrid(0: 0.1:100);
# 注意在绘图对象函数中，运算一般用点乘，点幂
z = x.^2 + y.^2 + sin(x.*y);
# 绘制等高线
contour(z,2)
# 创建一个三维曲面图
surf(x, y, z)

[x,y]=meshgrid(-4:0.1:4);
z = x.^2 + y.^2;
# 创建一个网格图，该网格图为三维曲面
mesh(x, y, z);
# 设置当前颜色图（有一些预设的方案提供）
colormap(hot)

matlab程序设计

1.if-else

编写求解方程根的函数

a = input('a值：');
b = input('b值：');
c = input('c值：');
t = b^2 - 4*a*c;

# 通过条件判断分流
# 每个if要用一个end结束
if a==0 && b==0
       disp('为恒不等式')

elseif a==0
       x = -c/b;
       disp(x)    
else        
    if t<0
        disp('该方程无解')
    elseif t==0
        x = -b/2*a;
        fprintf('x1=x2=%d',x);
    else
        x1 = (-b+sqrt(t))/2*a;
        x2 = (-b-sqrt(t))/2*a;
        fprintf('x1=%d\nx2=%d',x1,x2);
    end 
       
end

2.switch

输入一个百分制成绩，要求输出成绩等级

% 取整分级
sorce = input('请输入你的成绩：');
level = floor(sorce/10);

if sorce>100 || sorce <0
    disp('error')
end    

# matlab的switch不用break结束
switch level
    case 10
        disp('A+')
    case 9
        disp('A')
    case 8
        disp('B')    
    case 7
        disp('C') 
    case 6
        disp('D')
    otherwise
        disp('E')
end

3.for循环

利用for循环语句编写计算n!的函数程序

累加法时定义初始数为0

累积法时定义初始数为1

function[res] = work43(n)
    res = 1;
    if n<0
        res='error';
    elseif n == 0
        res = 0;
    else
        for i = 1:n
        res = res*i; 
        end   
    end    
end

4.构建Fibonacci数组

matlab的数组可以自动拓宽

a(1) = 1;
a(2) = 1;
k = 1;

while a(k) < 10000
    a(k+2) = a(k) + a(k+1);
    k = k + 1;
end

disp(a(k))

SIMULINK仿真

快速入门：https://ww2.mathworks.cn/help/simulink/getting-started-with-simulink.html

快速查询常用模块：https://www.cnblogs.com/dingdangsunny/p/12235689.html#_label1_2

一.simulink表示微分方程

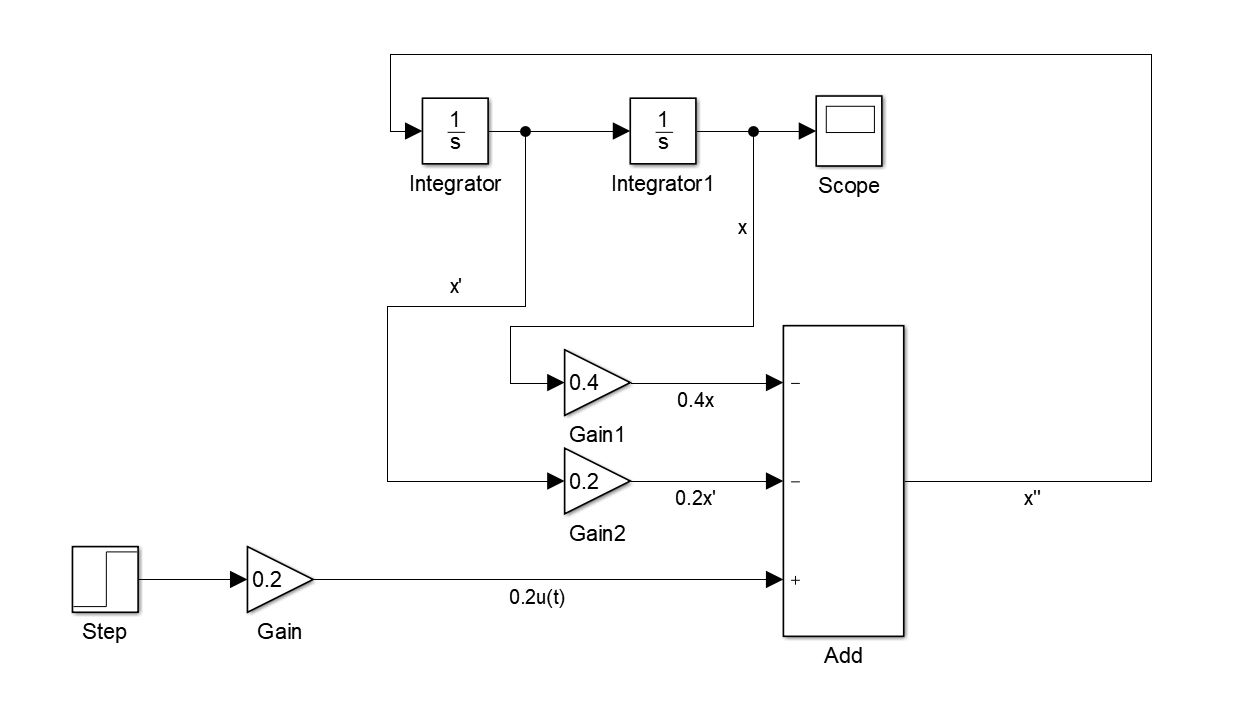
Step：跃迁信号
Gain：支持标量、向量或矩阵形式的增益。（可以看作是高级的乘法）
Add：加法模块（sum模块也很常用）
Integrator：积分模块
Scope：示波器波器