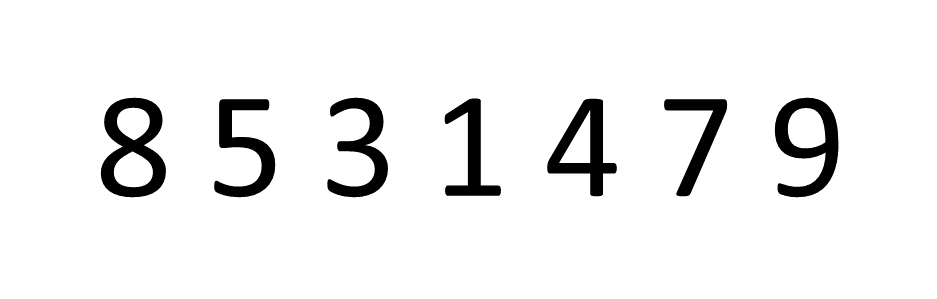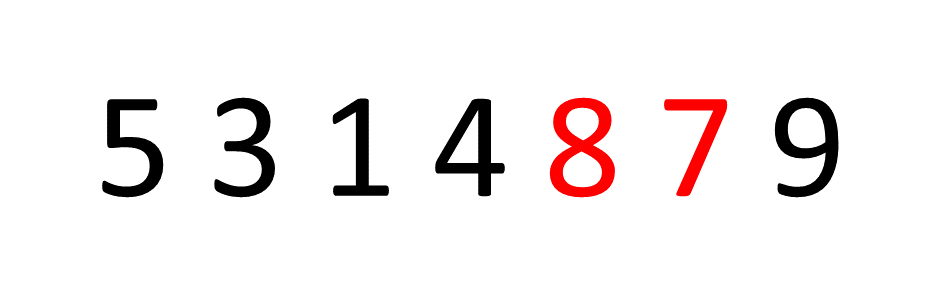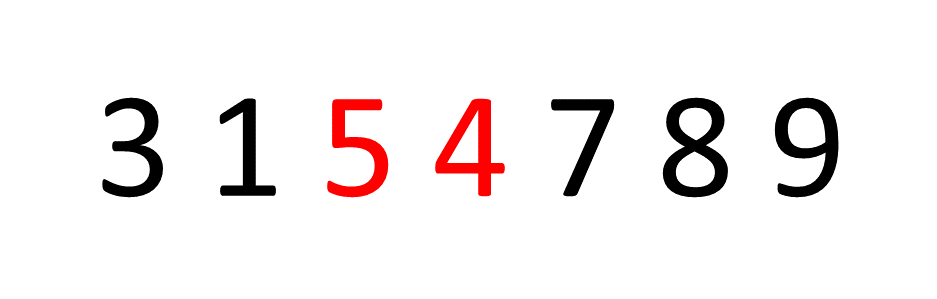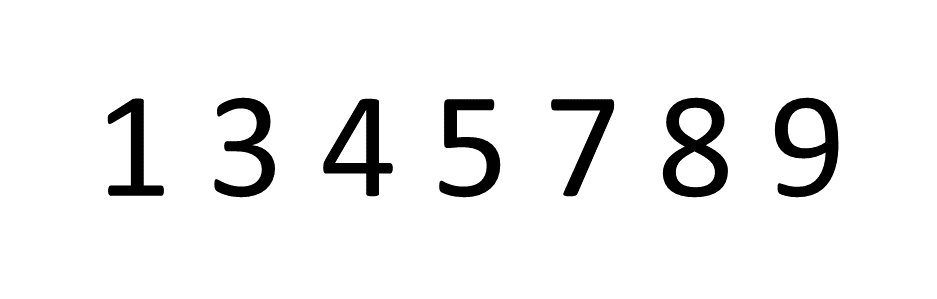Just For Interest

0%

C语言|算法入门指南

发表于 分类于 热度： Valine：
本文字数： 11k

image-20210210110218935

时间复杂度（Time complexity）

1.一个例子

情景：在一个有100个学生的教室里，仅有一名学生没过英语四级，我们要找到这名学生

  • 方法一：问每一个学生是否有过四级，时间复杂度为O(n)
  • 方法二：问每一个学生两个问题：1.是否有过四级 2.其他99个人过四级的情况，时间复杂度为O(n2)
  • 方法三：将100人分成两组，然后问没过四级的是在第一组还是在第二组，然后将该小组又分成两部分，再次询问，以此类推，直到最后找到没过四级的那个学生，时间复杂度为O(log n)

如果只有一个学生知道笔隐藏在哪个学生上，我可能需要进行O（n2）搜索。如果一个学生拿着笔，只有他们自己知道，我会使用O（n）。如果所有学生都知道，我会使用O（log n）搜索，但是只会告诉我是否猜对了。

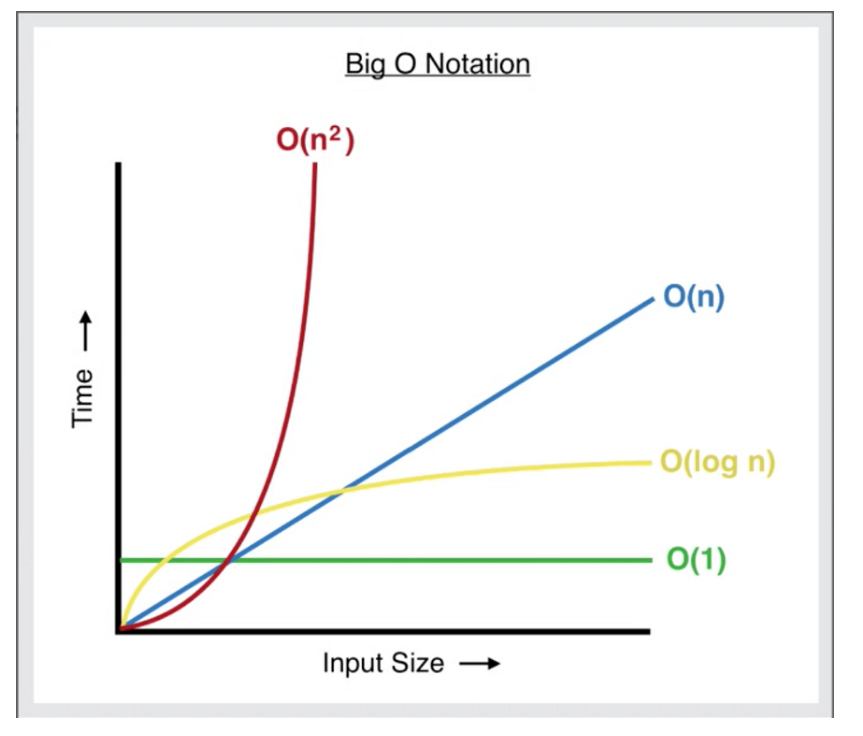
2.时间复杂度的含义

时间复杂度并不等于程序执行时间，我们没有考虑执行代码中每个语句所需的实际时间，而是考虑每个语句执行多少次

3.时间复杂度图示

image-20210210104634026

4.时间复杂度计算方法

  • 将算法/功能分解为单独的操作
  • 计算每个操作的复杂度
  • 将每个操作的复杂度加起来
  • 删除常量
  • 找到最高阶项-这就是我们认为算法/函数的复杂度

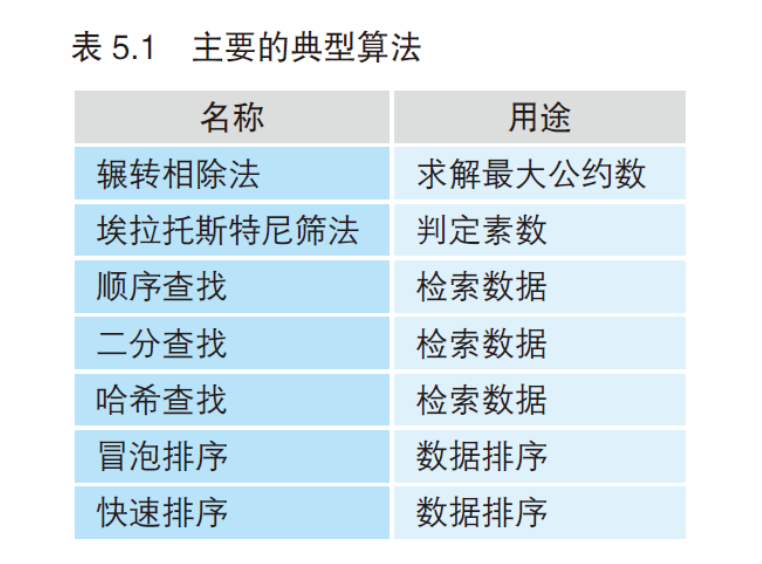
经典算法一览

image-20210210110218935

辗转相除法（Euclidean algorithm）

1.基本概念

  • 辗转相除法又称为欧几里得算法，常用于求解最大公约数
  • 算法原理：若a除以b的余数为r , 则有 gcd(a , b) = gcd( b ,r )
  • 算法思路：大数除于小数得余数，该余数再与小数重复上面步骤，直到最后得小数为0，这时大数即为最大公约数

2.基本案例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <stdio.h>

// 使用递归函数辗转相除返回最大公约数 
int gcd(int a, int b){
	
	if(a == 0){

		return b;		
	}
	
	return gcd(b%a, a);
	
}

// 结果展示 
int main(){
	
	int a = 10; 
	int b = 15;
	printf("GCD(%d, %d)=%d\n", a, b, gcd(a,b));
	
	a = 35; 
	b = 10;
	printf("GCD(%d, %d)=%d\n", a, b, gcd(a,b));
	
	a = 31; 
	b = 2;
	printf("GCD(%d, %d)=%d\n", a, b, gcd(a,b));	
	
}

语法解析：

  • b%a即b除以a后的余数，当b<a时，返回b，所以在以上程序中，我们不需要比较a，b大小，比如gcd(35,10) ,经过b%a会变成gcd(10,35)
  • 递归是一种特殊的循环，其停止的信号是return语句
  • 以上程序的时间复杂度是：O(Log min(a, b))

3.扩展案例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<stdio.h>
// gcd扩展版，不仅可以得到最大公约数，还可以找到整数系数x和y
// ax + by = gcd(a, b) 
int gcdExtended(int a, int b, int *x, int *y) {

	if(a==0){
		*x = 0;
		*y = 1;
		return b;
	} 
	
	// x1,y1存储递归调用的结果
	int x1,y1;
	int gcd = gcdExtended(b%a, a, &x1, &y1);
	
	// 更新x,y值 
	*x = y1 - (b/a) * x1;
	*y = x1;
	
	return gcd; 

} 

// 展示结果
int main(){
	
	int x, y;
	int a = 35;
	int b = 15;
	
	int g = gcdExtended(a, b, &x, &y);
	printf("a*%d + b*%d = %d ", x, y, g);
	return 0;
	
}

语法解析：

  • 以上程序目的是为了计算： ax + by = gcd(a, b) 中的x，y
  • 本程序使用了指针，可以在另一个函数中修改主函数的值，避免变量作用域的问题。在主函数内，可以通过&x,&y将x，y的地址传给其他函数，其他函数定义指针int *x, int *y存储地址，然后再用*x,*y读取地址中存的值即可修改主函数中的变量
  • int gcd = gcdExtended(b%a, a, &x1, &y1);使程序反复执行其上面的语句，直至a==0,这时可以得到gcd,和x1=0，y1=1的初始值。然后再开始与以上执行方向相反执行其下面的语句。最后return gcd实际上在第二部分的循环中，值不变
  • 主函数执行时，gcdExtended中的地址是主函数x，y的地址，而递归函数中的地址是x1，y1的地址;x1,y1存储的是上一个循环中的*x，*y

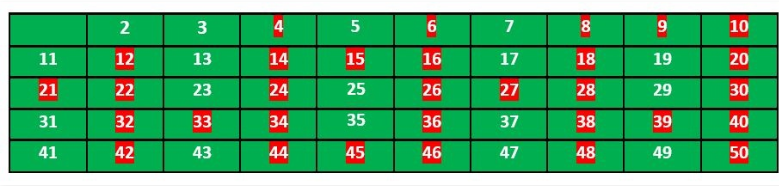
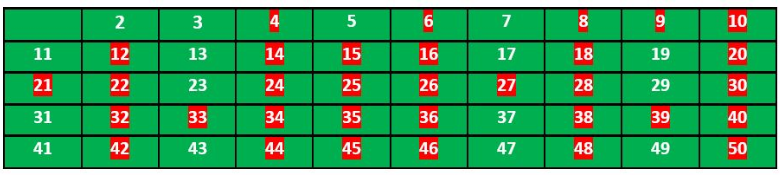
埃拉托斯特尼筛法（sieve of Eratosthenes）

1.基本概念

埃拉托斯特尼筛法是一种常用的素数筛法，可以筛选一定范围自然数内的质数（Prime numbers），时间复杂度：O(n log log n)

埃拉托斯特尼筛法演示动画（摘自维基百科）

img

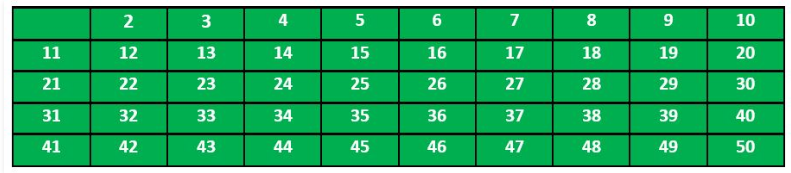
2.实现步骤

该筛法的基本步骤案例，筛选2-50范围内的素数

（1）创建2-50所有数字的列表

image-20210214200912413

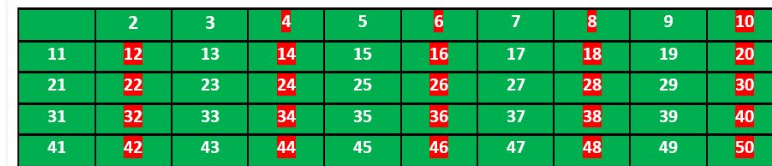
（2）标记所有2的倍数且大于或等于其平方（即4）的数字

image-20210214200920690

（3）标记所有3的倍数且大于或等于其平方（即9）的数字

image-20210214202117142

（4）标记所有5的倍数且大于或等于其平方（即25）的数字

image-20210214202159136

（5）标记所有7的倍数且大于或等于其平方（即49）的数字

​ 查无数字，则跳过这一步

（6）去掉列表中标记的数字，剩下的未被标记数字即为素数：2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.

3.基本案例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <stdio.h>
 
// 筛选素数函数
void  SieveOfEratosthenes(int n){
	
	// 创建标识数组
	bool primes[n+1]; 
	// 标识数组默认填入true,用索引当作自然数 
	for(int i = 2; i<=n; i++) {
		
		primes[i] = true;
		
	}
	
	// 开始标记非质数（即标记p的倍数且大于或等于其平方的数字） 
	for(int p=2; p*p<=n; p++){
		if(primes[p] == true){
			
			for(int i=p*p; i<=n; i+=p){
				primes[i] = false;
			}
			
		}
	} 
	
	// 打印出所有素数
	for(int p=2; p<=n; p++){
		if(primes[p]){
			printf("%d\n",p);
		}
	} 
	
	
}

int main(){
	
	int n;
	printf("输入筛选范围:");
	scanf("%d",&n);
	SieveOfEratosthenes(n); 
	return 0; 
	
}

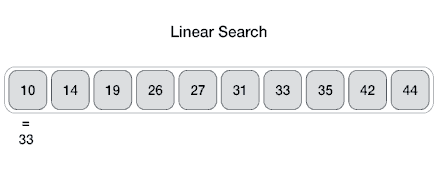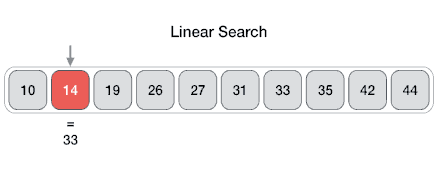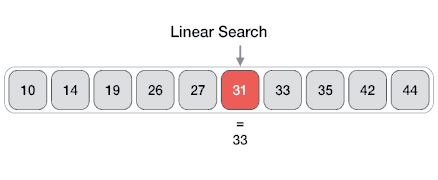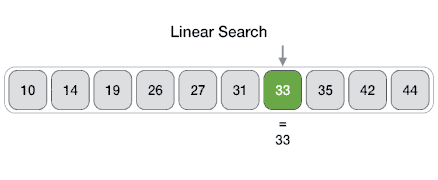
线性查找（Linear search）

1.基本概念

线性查找时间复杂度为：O(n)

线性查找的步骤如下：

  • 从arr []的最左边元素开始，然后将x与arr []的每个元素一一比较
  • 如果x与元素匹配，则返回索引。
  • 如果x与任何元素都不匹配，则返回-1。

线性查找示意图如下：

img

2.基本案例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <stdio.h>

// 线性查找函数
int search(int arr[], int n, int x){
	
	// 逐个遍历查找，n为数组长度 ，x为查找对象 
	for (int i=0; i<n; i++){
		
		if(arr[i]==x){
			return i;
		}
		
	}
	
	return -1;
	
} 


// 运行实例
int main(void){
	// 目标数组 
	int arr[] = {2, 3, 5, 10, 20, 40};
	
	// 查找目标
	int x = 10;
	
	// 测量数组大小
	int n = sizeof(arr) / sizeof(arr[0]);
	
	// 查找过程
	int result = search(arr, n, x);
	

	(result==-1)? printf("目标不存在"):printf("目标所在索引为%d", result);
	
	return 0; 
	
	
}

二分查找（Binary Search）

1.基本概念

二分查找的对象是从小到大的数组，其时间复杂度可以写作：O(Log n)

二分查找步骤：

  • 将x与中间元素比较
  • 如果x与中间元素匹配，则返回中间索引
  • 否则如果x大于中间元素则取中间元素后右半边数组重复操作
  • 否则如果x小于中间元素则取中间元素后左半边数组重复操作

二分查找示意图：

“Binary Search”

2.基本案例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <stdio.h> 
// 递归法二分查找
int binarySearch(int arr[], int l, int r, int x){
	
	if(r >= l){
		
		// 求中间元素
		int mid = l + (r - l) / 2; 
		
		// 情况1：如果目标与中间元素匹配 
		if(arr[mid] == x){
			return mid;
		}
		
		// 情况2:如果目标小于中间元素
		if(arr[mid] > x){
			// 返回以中间-1为右的递归 
			return binarySearch(arr, l, mid-1, x);
		} 
		
		// 情况3：如果目标大于中间元素
		// 返回以中间+1为左的递归 
		return binarySearch(arr, mid + 1, r, x);
		
	}
	
	// 查无结果
	return -1; 
} 

// 运行实例
int main(void){
	// 目标数组 
	int arr[] = {2, 3, 5, 10, 20, 40};
	
	// 查找目标
	int x = 10;
	
	// 测量数组大小
	int n = sizeof(arr) / sizeof(arr[0]);
	
	// 查找过程,定左右 
	int result =  binarySearch(arr, 0, n - 1, x);
	
	(result==-1) ? printf("目标不存在") : printf("目标所在索引为%d", result);
	
	return 0; 
		
}

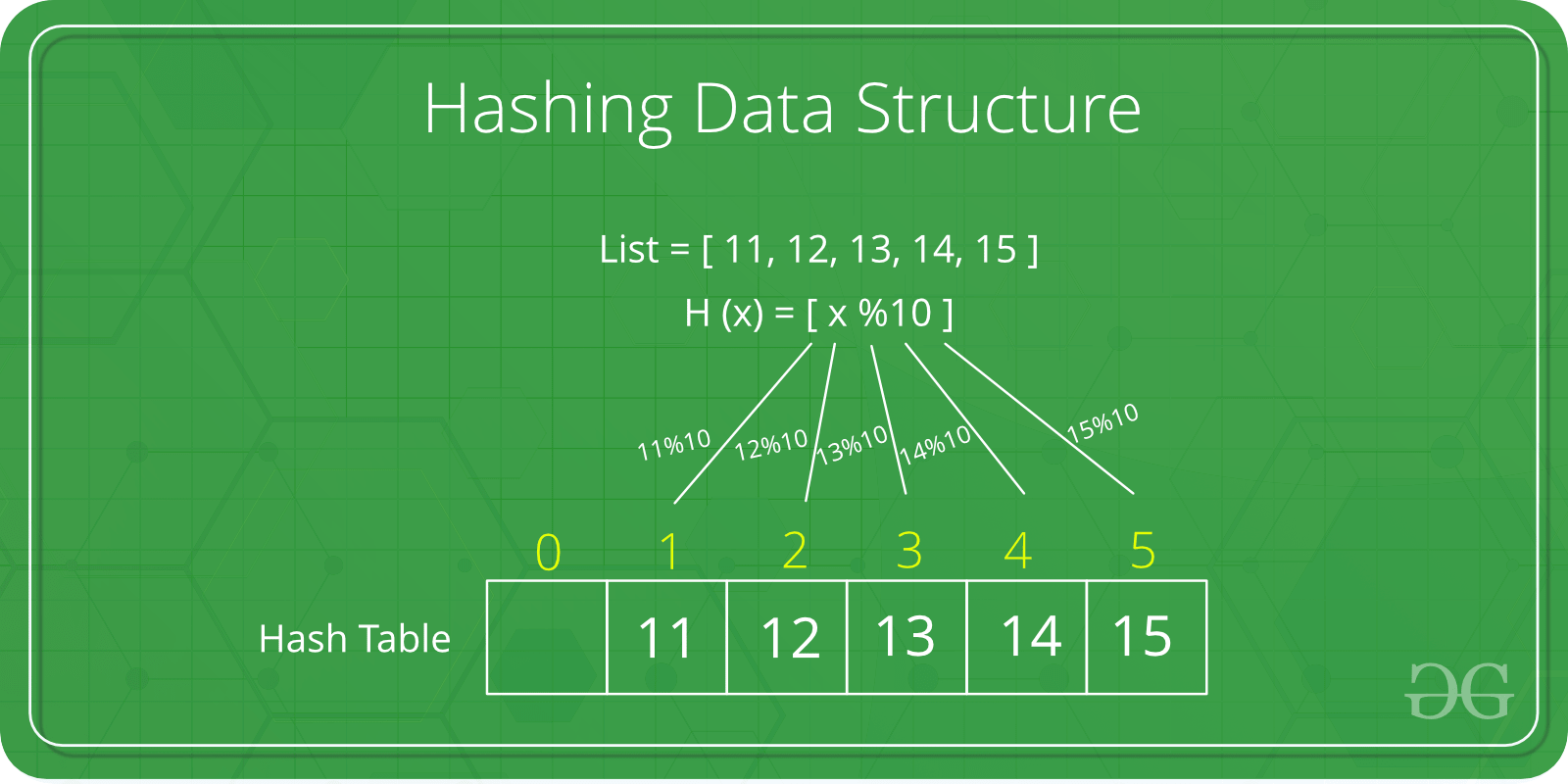
哈希表（Hash table）

1.基本概念

哈希表是一种数据结构，其以键值对的形式表示数据。每一个键都映射哈希表中的一个值（与关联数组类似）

在哈希表中，对键进行处理以生成映射到所需元素的新索引。此过程称为hashing。

哈希表是存储和检索元素的有效方法，所以其也是一种有效的查找算法

“hashing”示意图

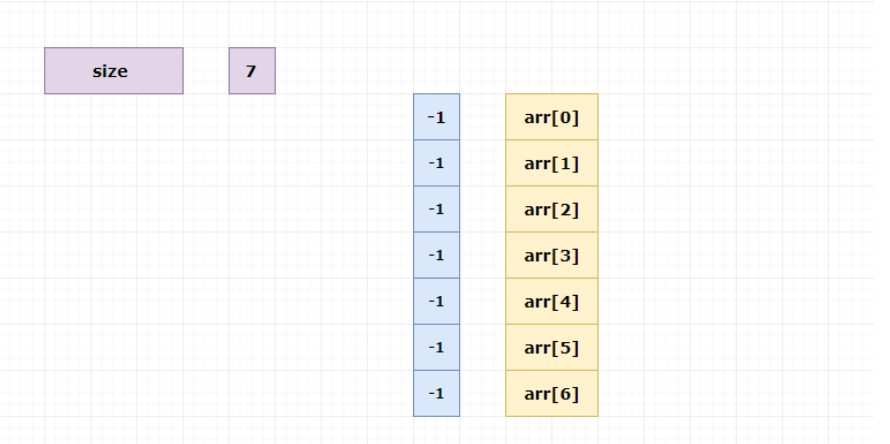
2.实现步骤

（1）哈希表初始化

​ 在将元素插入数组前，将数组默认值设为-1（-1表示元素不存 在或特定的索引可以插入）

​ image-20210215110519122

（2）插入元素

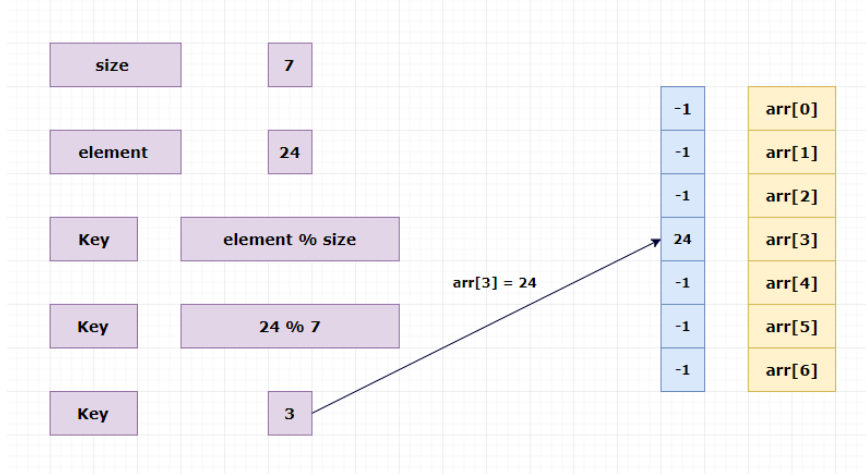
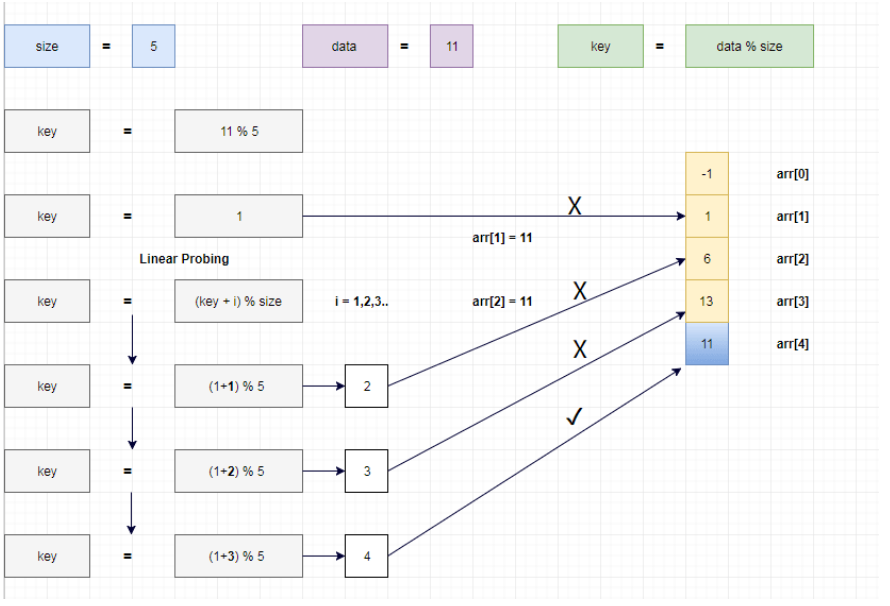
​ 哈希表插入元素的经典算法是：key = element % size （key即数据插入位置，element即元素，size即数组大小）

​ 如插入数字24

​ image-20210215111157606

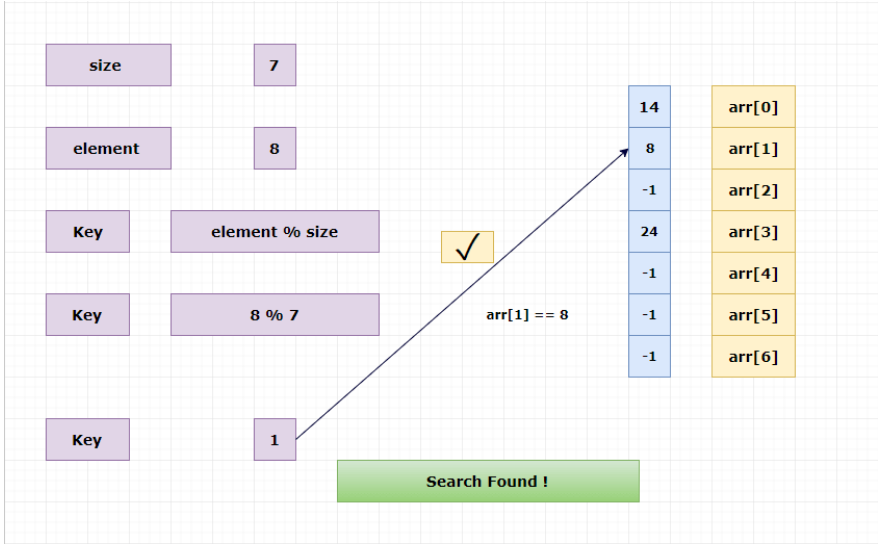
（3）搜索元素

搜索元素和插入元素使用同一算法获得索引（key），再按索引查找对应元素

image-20210215111443960

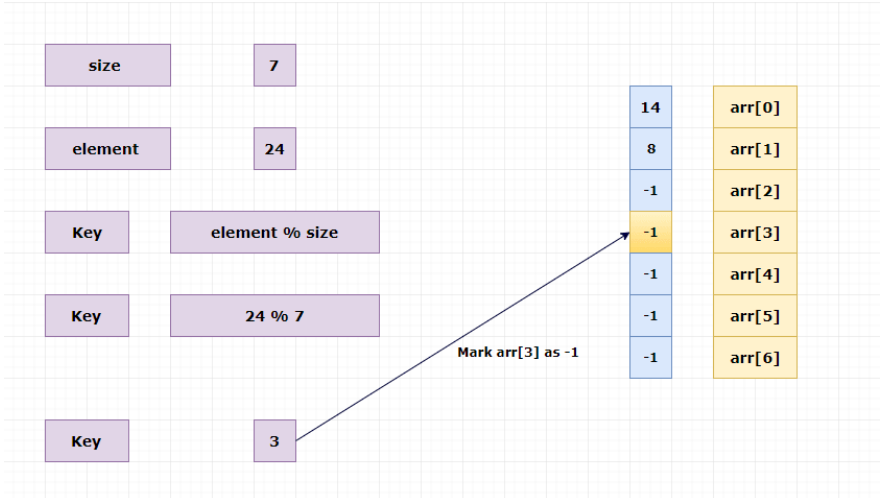
（4）删除元素

在哈希表中删除元素并不是指将数组中的元素移除，而是将元素的值初始化为-1

image-20210215111738024

3.基本案例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
# include <stdio.h> 
# define size 7 
 
// 创建数组作为基本结构
int arr[size]; 

// 哈希表初始化，将所有元素赋值为-1 
void init(){
	int i;
	for(i=0; i<size; i++){
		arr[i] = -1;
	}
} 

// 插入数据
void insert(int value){
	int key = value % size;
	
	if(arr[key] == -1){	
		arr[key] = value;
		printf("%d 插入到 arr[%d]\n", value, key);
	}
	
	else{
		printf("该位置存在冲突"); 
	}
	
	
}

// 删除数据 
void del(int value){
	int key = value % size;
	
	if(arr[key] == value){
		arr[key] = -1;
	}
	
	else{
		printf("该值不存在"); 
	}
	
} 

// 查询数据
void search (int value){
	int key = value % size;
	
	if(arr[key] == value){
		printf("查有此项"); 
	}
	
	else{
		printf("查无此项"); 
	}
	
} 

// 打印出所有数据
void print(){
	int i;
	for(i=0; i<size; i++){
		printf("arr[%d] = %d\n", i, arr[i]);
	}
} 

// 运行实例
int main(){
	// 初始化哈希表 
	init();
	
	// 填充哈希表  
	insert(10);
	insert(4);
	insert(2);
	insert(5); 
	
	// 打印哈希表
	printf("\n");
	print(); 
	
	// 删除测试
	printf("\n");
	del(5); 
	print();
	
	// 查询测试
	printf("\n");
	search(4); 
}

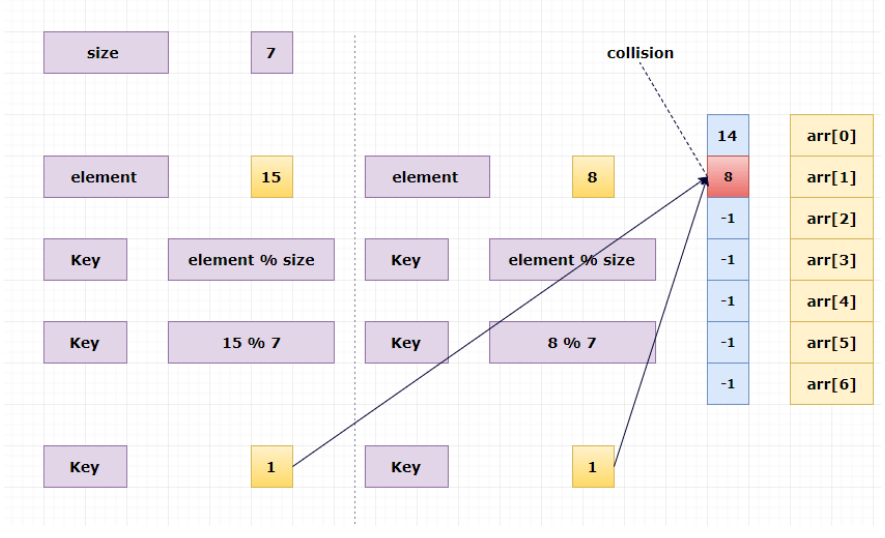
4.哈希冲突（collision）

如果存在插入元素算法得到得索引相同，会出现哈希冲突的情况

image-20210215151206845

以下介绍几种避免哈希冲突的方法

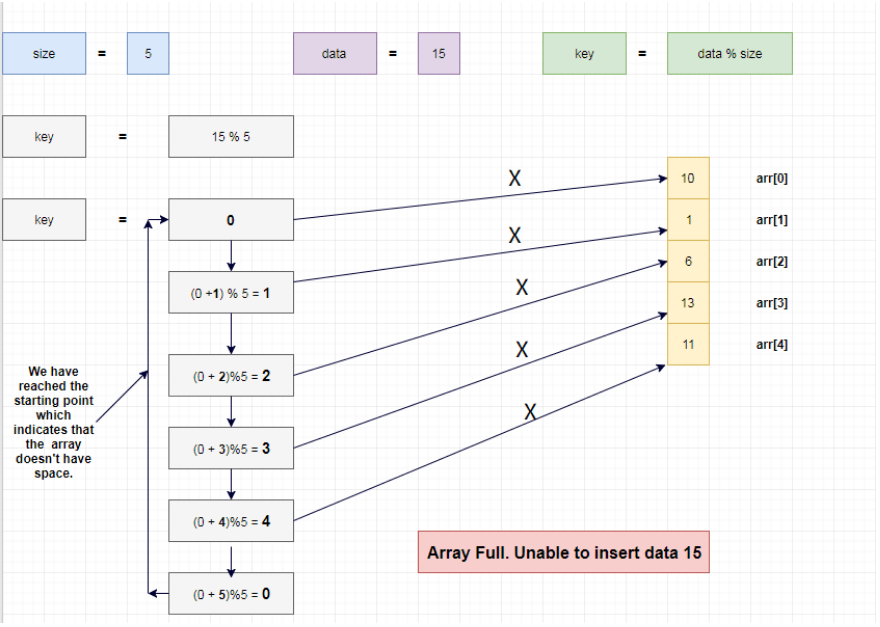
5.线性探测(Linear Probing)

（1）方法简介：通过key = element % size计算索引，如果该索引为空则直接填入，如果产生了冲突就检查下一个索引即key = (key+1) % size，重复执行该过程直到找到空间

（2）方法示意图

image-20210215153740661

空间不足的情况：

image-20210215154203024

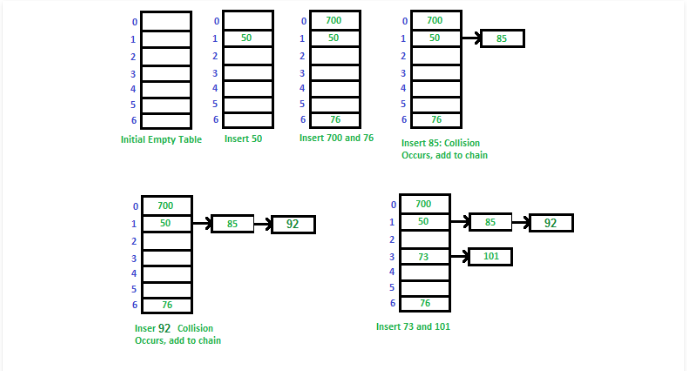
6.单独链表法（separate chaining）

（1）方法简介

单独链表法又被称为开放式哈希表（Open hashing），它采用数据结构中的链表（linked list）来解决哈希冲突的问题，这样的哈希表永远也不会被填满

这种方法使哈希表的每个单元指向具有相同索引值的链表

（2）方法示意图

image-20210215160449318

（3）使用案例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
# include<stdio.h>
# include<stdlib.h>

# define size 7

// 创建链表节点
struct node{
	// 存储该节点内容 
	int data;

	//  存储下一个节点的地址 
	struct node* next;
}; 

// 创建单独链表（每一个哈希表的索引一条链表）
struct node* chain[size];

// 哈希表初始化，每一列填入NULL 
void init(){
	int i;
	for(i=0; i<size; i++){
		chain[i] = NULL;
	}
} 

// 哈希表中插入元素 
void insert(int value){
	// 创造新节点存储数据
	struct node *newNode = (struct node*)malloc(sizeof(struct node));
	newNode->data = value;
	newNode->next = NULL;
	
	// 计算索引（hash key）
	int key = value % size;
	
	// 检查单独链表是否为空
	// 为空则填入新节点 
	if(chain[key] == NULL){
		chain[key] = newNode;
	} 
	// 不为空即产生了哈希冲突 
	else{
		// 需要在已有的末端节点后添加新节点
		// 获得指定索引的链表 
		struct node *temp = chain[key];
		
		// 遍历链表得到末端节点 
		while(temp->next){
			temp = temp->next; 
		} 
		
		// 在末尾连接上新节点 
		temp->next = newNode; 
		
	}
 
}

// 哈希表中搜索元素
int search(int value){
	int key = value % size;
	struct node *temp = chain[key];
	// 遍历链表寻找元素 
	while(temp){
		if(temp->data == value){
			return 1;
		}
		return 0;		
	}
} 

// 哈希表中删除元素
int del(int value){
	int key = value % size;
	// 存储头部节点 
	struct node *temp = chain[key],*dealloc;
	
	if(temp != NULL){
		// 如果需要删除的元素在头部 
		if(temp->data == value){
			dealloc = temp;
			temp = temp->next;
			free(dealloc);
			return 1; 
		}
		else{
			// 遍历链表寻找需要删除的元素 
			while(temp->next){
				if(temp->next->data == value){
					dealloc = temp->next;
					temp->next = temp->next->next;
					free(dealloc);
					return 1; 
				}
				temp = temp->next;
			}
		}
	}
	 
	return 0; 
} 

// 打印哈希表
void print() {
	int i;
	
	for(i=0; i<size; i++){
		struct node *temp = chain[i];
		printf("chain[%d]-->",i);
			
		// 打印链表	
		while(temp){
			printf("%d-->", temp->data);
			temp = temp->next;
		}
		
		printf("NULL\n");
	}
}

// 运行实例
 int main(){
 	// 初始化哈希表
	init();
	 
	// 填充数据
    insert(7);
    insert(0);
    insert(3);
    insert(10);
    insert(4);
    insert(5);  
 	printf("\n");
 	print(); 
 	
	printf("\n");
	// 删除测试
	if(del(10)){
		print(); 
	}  
	else{
		printf("删除项不存在");
	}
 	
 	return 0;
 }

冒泡排序（Bubble Sort）

1.基本概念

（1）冒泡排序通过重复交换错误顺序的两个数来工作

（2）冒泡排序步骤：

  • 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  • 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
  • 针对所有的元素重复以上的步骤，除了最后一个。
  • 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

（3）冒泡排序示意图:

“Bubble Sort gif”的图片搜索结果

2.基本案例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<stdio.h>

// 交换数字函数(此处的参数为地址，可以直接修改主函数中的值)
void swap(int *xp, int *yp){
	int temp = *xp;
	*xp = *yp;
	*yp = temp;
} 

// 冒泡函数
void bubbleSort(int arr[], int n){
	int i, j;
	// 从头开始的次数 
	for(i=0; i<n-1; i++){ 
	    // 移动读取数组相邻两个数 
		for(j=0; j<n-i-1; j++){
			// 符合条件，交换数值 
			if(arr[j]>arr[j+1]){
				swap(&arr[j], &arr[j+1]);
			}
		}
	}
} 


// 打印数组函数
void printAarry(int arr[], int size){
	int i;
	for(i=0; i<size; i++){
		printf("%d ", arr[i]);	
	}
	printf("\n");
} 


// 运行实例
int main(){
	int arr[] = {64, 34, 25, 12, 22, 11, 90}; 
	// 计算数组大小 
	int n = sizeof(arr) / sizeof(arr[0]);
	// 冒泡处理 
	bubbleSort(arr, n);
	
	printf("排序后的数组：\n");
	printAarry(arr, n);
	return 0;
}

快速排序（Quick sort）

参考文章：https://juejin.cn/post/6844904122538278920

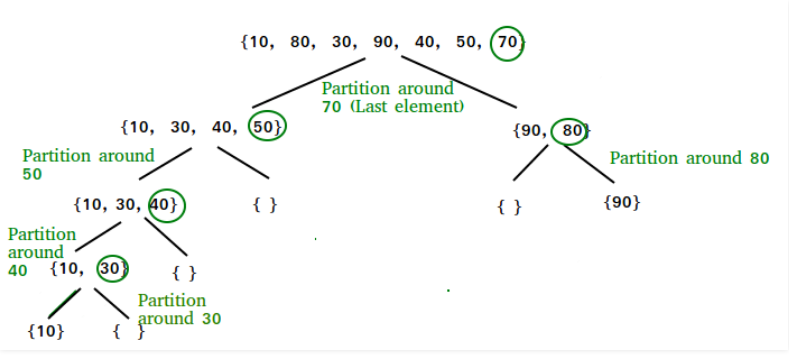
1.基本概念

（1）快速排序是一种分而治之的算法，它会一个元素为枢纽键对数组进行分区，枢纽有以下几种选择，本文以最简单的最后一个元素为枢纽为例

  • 始终选择第一个元素作为枢轴
  • 始终选择最后一个元素作为枢轴
  • 选择一个随机元素作为枢轴。
  • 选择中位数作为枢轴

（2）实现步骤

  • 在给定数组中确定一个元素x作为枢纽
  • 将x放在排序数组中的正确位置
  • 将小于x的元素放在x之前
  • 将大于x的元素放在x之后
  • 去掉枢纽分成两组后重复以上操作

以末尾元素为枢纽排序示意图

image-20210226194704522

​ （3）将小于x的元素放在x之前，将大于x的元素放在x之后这一步是将一个数组分成两个数组，其运用到了分而治之的思想

  • 将一个数组分成两个数组的方法为：
    先从数组右边找到一个比枢轴元素小的元素，将数组的第一个位置赋值为该元素；

  • 再从数组的左边找到一个比枢轴元素大的元素，将从上面取元素的位置赋值为该值；

  • 依次进行，直到左右相遇，把枢轴元素赋值到相遇位置。

    示意图如下：

第一轮排序动态过程

2.基本案例

基本案例中也运用了分而治之的方法，当操作步骤与上面步骤相异但是效果相同

  • 选择最后一个元素作为枢纽
  • 从数组左端开始遍历一个数组，先设最左端元素为待交换元素。当遇到比枢纽值小的元素，就将其与待交换元素值相交换，并把下个元素设为待交换元素
  • 完成遍历后，最后交换末尾元素与待交换元素，并返回待交换元素的索引
  • 依据返回的索引将数组分成了两组：左边比枢纽元素小，右边比枢纽元素大
  • 最后再递归分开处理左边数组和右边数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<stdio.h>

void quickSort(int[], int, int);
int  partition(int[], int, int);
void swap(int*, int*);

int main()
{
    int n,i;

    printf("数组大小\n");
    scanf("%d",&n);

    int arr[n];

    printf("填入数组数据\n");
    for(i=0;i<n;i++)
        scanf("%d",&arr[i]);

    quickSort(arr,0,n-1);

    printf("快速排序后的数组\n");

    for(i=0;i<n;i++)
        printf("%d ",arr[i]);
    printf("\n");

    return 0;
}

void quickSort(int arr[], int start, int end)
{
    if(start < end)
    {
        int pIndex = partition(arr, start, end);
        quickSort(arr, start, pIndex-1);
        quickSort(arr, pIndex+1, end);
    }
}

int partition(int arr[], int start, int end)
{
    int pIndex = start;
    int pivot = arr[end];
    int i;
    for(i = start; i < end; i++)
    {
        if(arr[i] < pivot)
        {
            swap(&arr[i], &arr[pIndex]);
            pIndex++;
        }
    }
    swap(&arr[end], &arr[pIndex]);
    return pIndex;
}

void swap(int *x, int *y)
{
    int t = *x;
    *x = *y;
    *y = t;
}

*y = t;
}