Just For Interest

0%

C语言|数据结构入门指南

发表于 分类于 热度： Valine：
本文字数： 7.7k

image-20210205093243144

数据结构入门指南（C语言版）

（图片来源于《计算机是怎么跑起来的》一书和GeeksforGeeks网站）

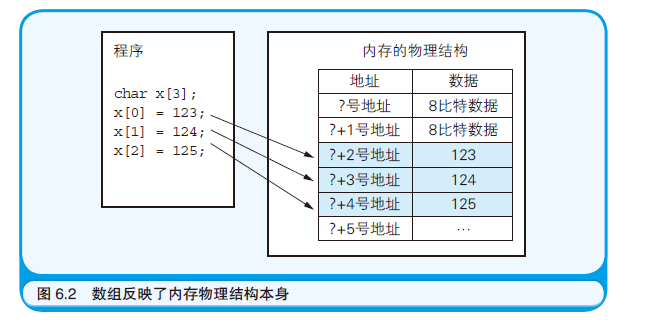
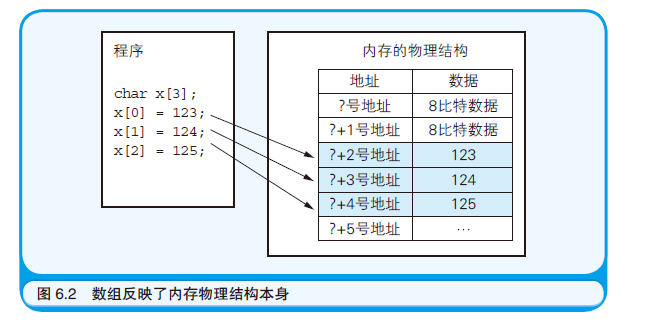
初识数据结构

1.数组

数组是数据结构的基础。

数组在程序中往往是从内存整体中分配出一块连续的空间，数组反映了内存的物理结构

image-20210205093243144

2.数组的应用

以数组为基础的数据结构，可供各种各样的算法处理大量数据

3.数据结构概念

内存的物理结构无法改变，而数据结构可以通过程序在逻辑上改变内存的物理结构，使数据按照自己的相反分布

典型的数据结构如下：

image-20210205094134834

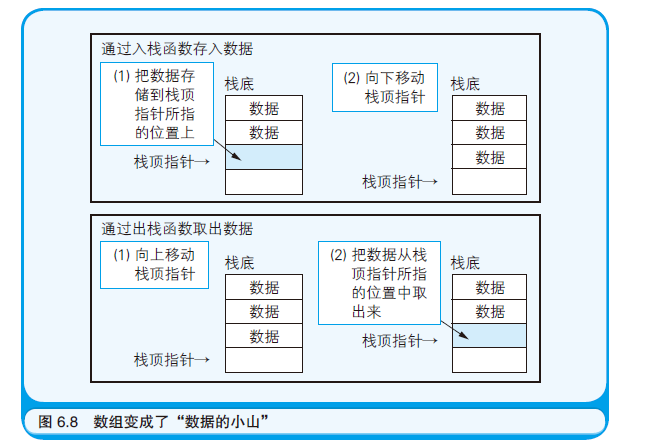
栈的实现方法（stack）

1.栈的特点

栈中数据的使用顺序和堆积顺序是相反的，堆积顺序是从下到上，而使用顺序是从上到上，就好像干草堆一样

image-20210205095057769

这种数据存取方式称为LIFO（last in first out，后进先出），即最后存入的数据最先被处理

2.栈的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <stdio.h>
// 构建数组作为栈的本体 
char Stack[100];
// 栈顶指针，始终指向栈数据的最顶端 
char StackPointer = 0; 

// 入栈函数，存储数据 
void Push(char Data){
	// 数据存储在栈顶指针指向位置 
	Stack[StackPointer] = Data;
	
	// 更新栈顶指针的值 
	StackPointer++;
}

// 出栈函数，读取数据 
char Pop(){
	
	// 更新栈顶指针的值 
	StackPointer--;
	// 在栈顶指针处取出数据 
	return Stack[StackPointer];
}
 
// 运行实例 
int main()
{	
	//存储数据 
	Push(1);
	Push(2);
	Push(3);
	Push(4);
	
	//读取数据 
	while (StackPointer !=0) {
		char result = Pop();
		printf("%d\n",result);
}

}
3.原理图

image-20210205104130629

注意此图的栈底放在上面，最底部才是栈顶

4.语法解释
  • 最终实现效果是：存入顺序是1，2，3，4；取出顺序是4，3，2，1
  • 栈的成分：数组，栈顶指针，入栈函数，出栈函数
  • 入栈函数将数据压入栈中
  • 出栈函数将数据从栈中弹出
  • 存储5个数据，最后栈顶指针指向5的地址（地址4为最后一个数据），所以在出栈函数中，栈顶指针需要减1，才能取得第一个数据

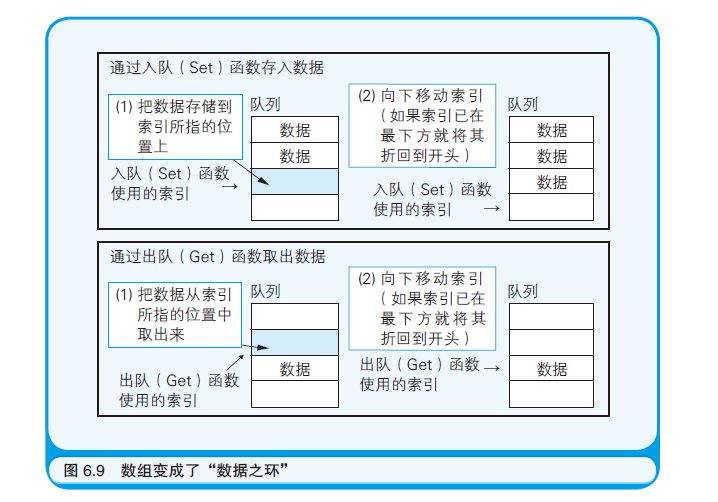
队列的实现方法（queue）

1.队列的特点

队列中最先存入的数据是被最先处理的，这种方式被称为FIFO（first in first out, 先进先出）。就像排队上车一样，先到的人就能先上车

image-20210205154955234

2.队列的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<stdio.h> 

// 构建作为队列本质的数组 
char  Queue[100];
// 标识数据存储位置的索引 
char SetIndex = 0;
// 标识数据读取位置的索引 
char GetIndex = 0;

 // 存储数据函数 
 void Set(char Data){
 	// 存入数据
	 Queue [SetIndex] = Data;
	 
	 // 更新存储索引 
	 SetIndex++;
	  
	 // 到达数组末尾则折回开头 
	 if(SetIndex>=100){
	 	SetIndex = 0;
	 } 
 }
 
 // 读取数据函数 
 char Get(){
 	char Data;
 	
	 // 读取数据 
 	Data = Queue[GetIndex];
 	
 	// 更新读取索引 
 	GetIndex++;
 	
 	//  到达数组末尾则折回开头 
 	if(GetIndex>=100){
 		GetIndex = 0;
	 }
	
	// 返回读出数据 
	return Data;
 }
 
 
 // 运行实例 
int main()
{	
	//存储数据 
	Set(1);
	Set(2);
	Set(3);
	Set(4);
	
	//读取数据 
	while (GetIndex != SetIndex) {
		char result = Get();
		printf("%d\n",result);
}

}
3.原理图

image-20210205161354653

4.语法解释
  • 最终实现效果是：存入顺序是1，2，3，4；取出顺序是1，2，3，4
  • 栈的成分：数组，数据存储指针，数据读取指针，存储函数，读取函数
  • 队列的逻辑结构实际上是圆环，数据存满后又会回到开头开始存数据
  • 数据读取指针和数据存储指针是一样的，走向一样，最终值（指存完数据和读完数据的最后值的值）也要相等

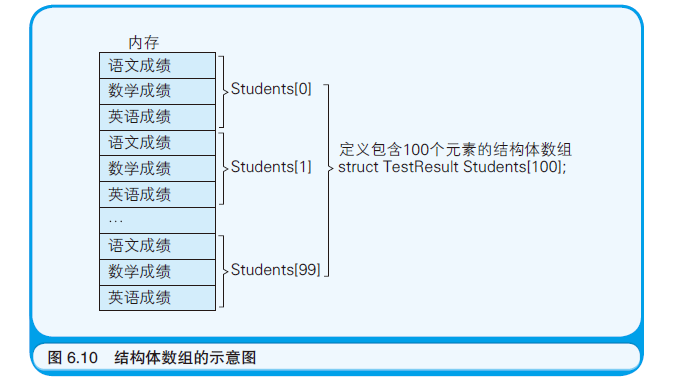
结构体

1.组成

结构体即把若干个数据项汇集到一起并赋予其名字的一个整体

定义完结构体后，我们可以把结构体当作一个数据类型，可以用它来声明变量

每一个被汇集到结构体的每一个数据项叫做结构体的成员

2.运用

我们需要用到结构体数组来实现链表和二叉树

3.内存分布

image-20210205182952994

链表的实现方法（Linked list）

1.链表的特点

链表容易实现数据的插入和删除，任意改变数据的排列方式。就像人手拉手排成一排，要改变顺序，只需要改变牵手对象即可实现

image-20210205183938605

2.链表的实现

参考文章：https://www.geeksforgeeks.org/linked-list-set-1-introduction/等系列文章

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
#include <stdio.h> 
#include <stdlib.h> 

//链表操作函数声明
void printList(struct Node* n); 
void insertAfter(struct Node* prev_node, int new_data);
void push(struct Node** head_ref, int new_data);
void append (struct Node**head_ref, int new_data);
void deleteNode(struct Node**head, int key) ;



// 创建链表节点
struct Node{
	// 存储该节点内容 
	int data;

	//  存储下一个节点的地址 
	struct Node* next;
}; 

// 程序简单创建一个三节点链表
int main(){
	// 声明节点 
	struct Node* head = NULL;
	struct Node* second = NULL;
	struct Node* third = NULL;
	
	// 为三个节点分配空间
	head = (struct Node*)malloc(sizeof(struct Node)); 
	second = (struct Node*)malloc(sizeof(struct Node)); 
	third = (struct Node*)malloc(sizeof(struct Node)); 
	
	
	// 在节点内存入数据（内容+下个节点的地址）构成链表
	head -> data = 1;
	head -> next = second; 
	
	second -> data = 2;
	second -> next = third;
	
	third -> data = 3;
	third -> next = NULL;
	
	// 最末端插入6，则链表为 1->2-> 3->6->NULL
	append(&head,6);
	
	// 在最前端插入7， 则链表为 7->1->2-> 3->6->NULL
	push(&head,7);
	 
	// 在指定位置（第三个节点的下个节点后面）插入8， 则链表为 7->1->8->2->3->6->NULL
	insertAfter(head->next,8);
	
	// 删除2
	deleteNode(&head, 2); 
	 
	printList(head); 
	
	return 0;
} 



// 从指定位置开始遍历链表函数
void printList(struct Node* n){
	// 链表的末尾一定指向NULL 
	while(n != NULL){
		printf("%d\n", n->data);
		n = n->next;
	}
}
 
// 链表插入有三种形式：1. 在最前面插入 2.指定位置插入  3. 在最末尾插入

// 1.在最前面插入
// 两个参数分别的含义是： 给定头的引用（指向指针的指针），插入的数据 
void push(struct Node** head_ref, int new_data){
	
	// （1）为新节点分配空间 
	struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
	
	// （2）放入数据
	new_node->data = new_data; 
	
	// （3） 新节点存储原头部的地址
	new_node->next = (*head_ref);
	
	// (4) 移动头部指向新节点，新节点成为新头部
	(*head_ref) = new_node; 
	
	
} 

// 2.在指定节点后面插入
void insertAfter(struct Node* prev_node, int new_data){
	
	// （1）检查给定节点是否为空
	if(prev_node==NULL){
		printf("error");
		return;
	} 
	
	// (2)为新节点分配空间 
	struct Node* new_node = (struct Node*) malloc(sizeof(struct Node));
	
	// (3)放入数据
	new_node->data = new_data;
	
	// (4)新节点存储插入节点存储的下个节点的地址
	new_node->next = prev_node->next;
	
	// 插入节点存储新节点的地址
	prev_node->next = new_node; 
	
	
} 
 
 
// 3.在最末尾插入
void append (struct Node**head_ref, int new_data){
	
	//	(1) 为新节点分配空间 
	struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
	// 第5步中使用 ,让第五步的找尾部从头部开始 
	struct Node *last = *head_ref;
	
	// (2) 放入数据
	new_node->data = new_data;
	
	// (3)  新节点要放到最后，所以存储地址为NULL
	new_node->next = NULL; 
	
	// (4) 如果链表为空，则新节点成为头部
	if(*head_ref == NULL){
		
		*head_ref = new_node;
		return;
	
	}
	
	// (5) 链表不为空，一直摸到链表末端
	while(last->next != NULL){
		last = last->next;
	} 
	
	// (6) 原末端节点存储的地址改为新节点
	last->next = new_node;
	return; 
	 
} 


// 删除给定值所在节点 
void deleteNode(struct Node**head_ref, int key) {
 
 // 存储头部节点
 struct Node *temp = *head_ref, *prev;
  
// 如果头部节点含有给定值，需要删除头部
if(temp != NULL && temp->data == key){
	// 改变头部
	*head_ref = temp->next; 
	
	// 释放旧头部
	free(temp);
	
	return; 
} 

// 遍历节点，搜索给定值的位置  
while(temp != NULL && temp->data !=key){
	prev = temp;
	temp = temp->next;
}

// 如果给定值不存在
if(temp == NULL){
	return;
} 

// 找到位置后，开始删除操作
// 移动删除节点前一个节点的链接到删除节点的下一个节点
prev->next = temp->next;

// 释放需要删除的节点
free(temp); 

}
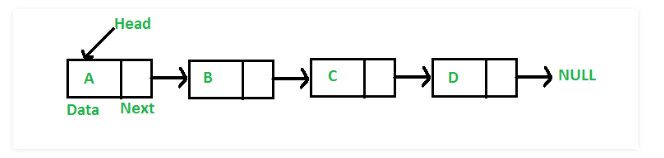
3.原理图

（1）链表结构图

image-20210208081719442

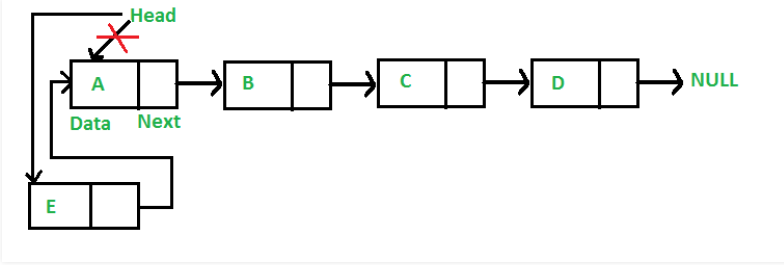
（2）头部插入示意图

image-20210208081851924

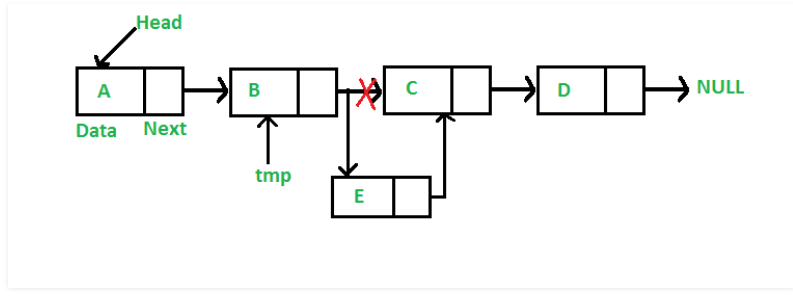
（3）指定位置插入示意图

image-20210208081923801

（4）末端插入示意图

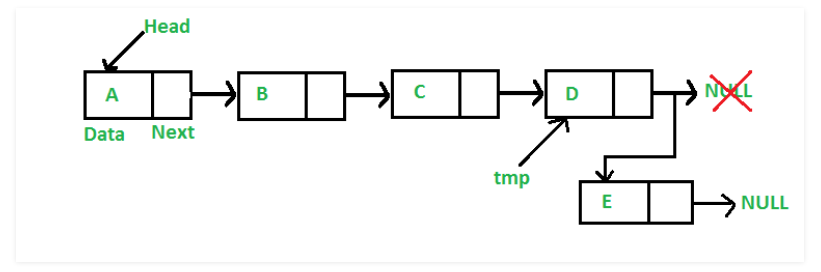
image-20210208082016685

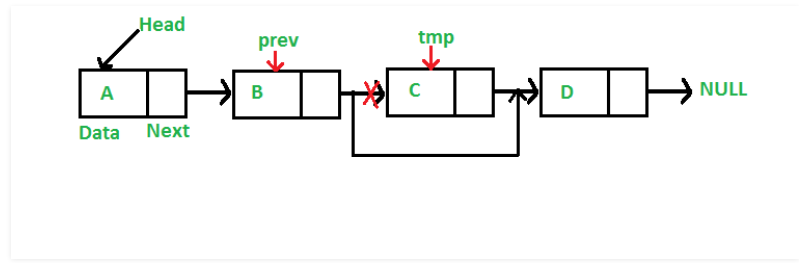
（5）删除示意图

image-20210208082128253

4.语法解释

  • struct Node* next声明后，next存储地址，*next是地址中的值（自我引用结构体）

  • 声明节点中，struct Node* head = NULL，则head内为地址

  • malloc()函数的声明方法为：void *malloc(size_t size)，其作用是分配所需的内存空间，返回值即为指向被分配内存的指针（地址）

  • 则有head，second，third存储的是指向该节点的指针（地址），要使指向该节点的指针访问到节点的成员，那就用->运算符

  • struct Node** head_ref相当于指向该结构体的指针的指针，即该指针存放的位置，相当于head（头部指针）取址即&head；* head_ref则为该结构的指针（即head，但是*head_ref这种方式才能动态移动指针）

二叉树的实现方法（Binary tree）

1.二叉树的特点

二叉树是基于链表的，用到的还是自我引用的结构体，但是会带有两个连接信息（即指向其他元素的指针）

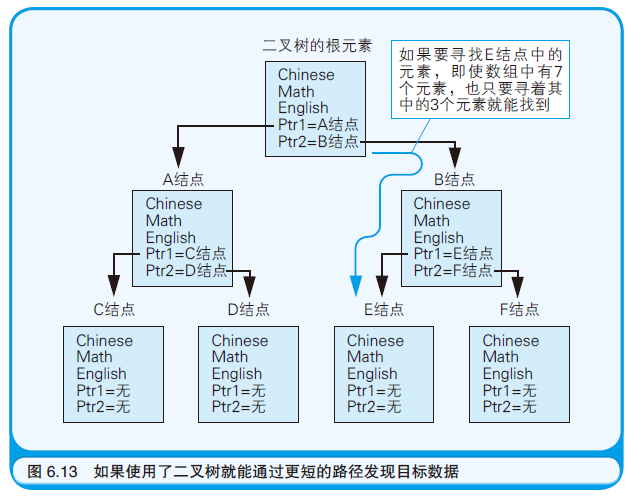
二叉树多用于实现用于搜索数据的算法（如：二分查找法）

二叉树结构在搜索数据时，不是沿着一条线搜索，而是循着二叉树的分叉不断向下搜索

image-20210208095901708

2.二叉树的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
#include <stdio.h>
  #include <stdlib.h>

  struct node{
  	int data;
  	struct node* left;
  	struct node* right;
  };
  
  // 声明操作二叉树的函数
  void printPostorder(struct node* node); 
  void printInorder(struct node* node);
  void printPreorder(struct node* node);
  
  
  
  
  // 创建一个新节点函数
  // 返回值为该节点的地址 
  struct node* newNode(int data){
  	
  	// 分配空间给新节点 
  	struct node* node = (struct node*)malloc(sizeof(struct node));
  	
  	// 分配数据给该节点
  	node->data = data;
  	 
  	// 初始左右分叉的指向
  	node->left = NULL;
  	node->right = NULL;
  	
  	return (node);   
  		
  }
  
  int main(){
  	
  	// 创建二叉树的首节点（root）
  	struct node* root = newNode(1);
  	
  	// 从首节点出发分叉出两页 
  	root->left = newNode(2);
  	root->right = newNode(3); 
  	
  	root->left->left = newNode(4);
  	root->left->right = newNode(5);
  	
  	printf("后序顺序打印\n");
  	printPostorder(root); 
  	printf("\n") ;
  	printf("中序顺序打印\n");
  	printInorder(root); 
  	printf("\n") ;
  	printf("前序顺序打印\n");
  	printPreorder(root); 
  	
  	
  }
  
  // 3种遍历方法 
  // 1.后序遍历 （左->右->根） 
  void printPostorder(struct node* node){
  	
  	if(node==NULL){
  		return;
  	}
  	
  	printPostorder(node->left);
  	printPostorder(node->right); 
  	
  	// 打印出该节点的数据 
  	printf("%d", node->data); 
  } 
  
  // 2.中序遍历（左->根->右）
  void printInorder(struct node* node){
  	
  	if(node==NULL){
  		return;
  	}
  	
  	printInorder(node->left);
  	printf("%d", node->data);
  	printInorder(node->right);
  	
  	
  } 
  
  //  3. 前序遍历 (根->左->右)
   void printPreorder(struct node* node){
   	
  	if(node == NULL){
   		return;
  	 }
  	 
  	printf("%d", node->data);
  	printPreorder(node->left);
  	printPreorder(node->right);
   	
   }
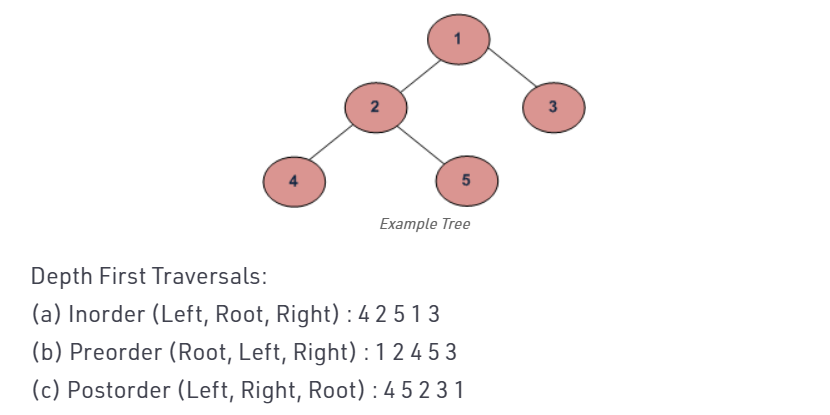
3.二叉树原理图

（1）遍历方法示意图

image-20210208150838184